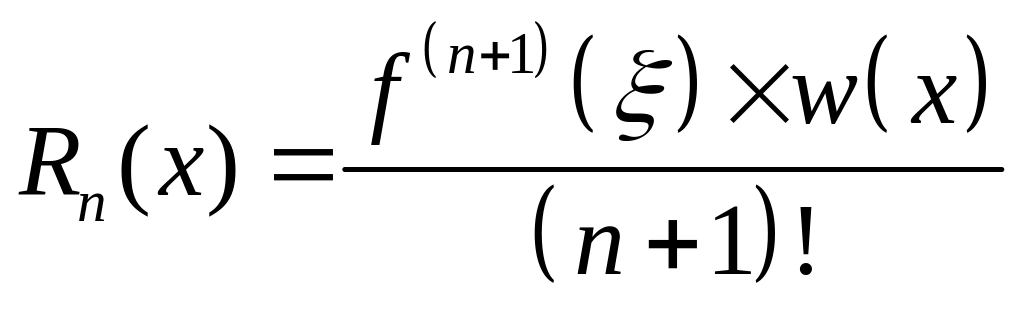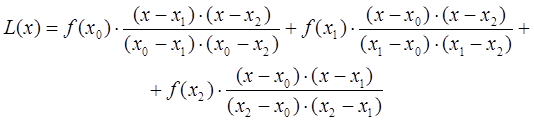Интерполяционный многочлен Лагранжа
Постановка задачи интерполирования. Полином Лагранжа, Стирлинга, Бесселя, Ньютона. Обратное интерполирование. Один из возможных путей решения поставленной задачи заключается в следующем:.










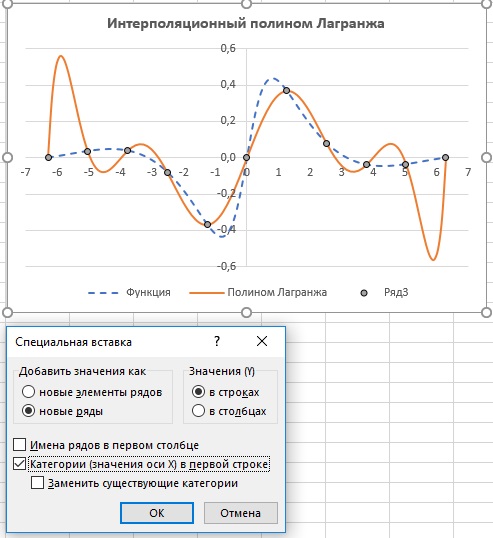
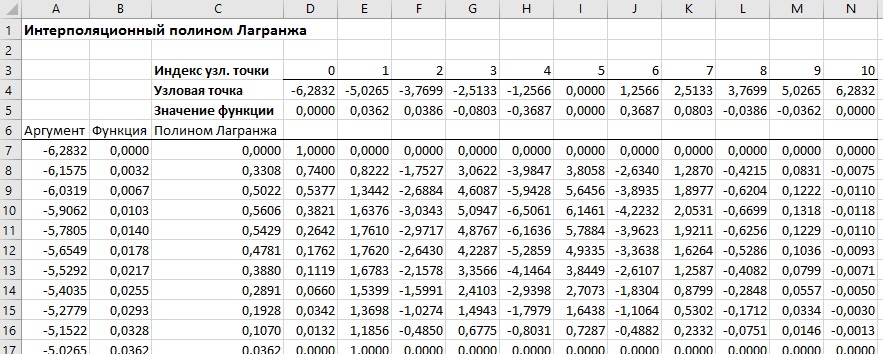
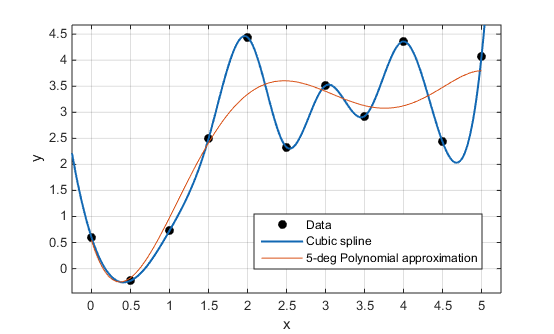
Выборка экспериментальных данных представляет собой массив данных, который характеризует процесс изменения измеряемого сигнала в течение заданного времени либо относительно другой переменной. Для выполнения теоретического анализа измеряемого сигнала необходимо найти аппроксимирующую функцию, которая свяжет дискретный набор экспериментальных данных с непрерывной функцией - интерполяционным полиномом n-степени. Одним из способов представления данного интерполяционного полинома n-степени может быть использован многочлен в форме Лагранжа. Интерполяционный многочлен в форме Лагранжа — это математическая функция позволяющая записать полином n-степени, который будет соединять все заданные точки из набора значений, полученных опытным путём или методом случайной выборки в различные моменты времени с непостоянным временным шагом измерений.
- Нужно пройти преддипломную практику у нескольких предметов написать введение и отчет по практике так де сдать 4 экзамена после практики.
- Постановка задачи интерполирования. Полином Лагранжа, Стирлинга, Бесселя, Ньютона.
- Интерполяционная формула Лагранжа это один из наиболее распространенных способов построения интерполяционного полинома. Пусть имеем функцию:.
- В работе рассматривается кусочно-интерполяционное приближение функций одной вещественной переменной с помощью интерполяционных полиномов Лагранжа и Ньютона.